RED-BLACK TREES -(i)

RED-BLACK TREES -(i)

Red-black tree is a binary search tree with one extra property for a given node. This extra property is the color which can be either red or black. This property does not have to be represented as a color object always. It can be a integer with 1 representing black and 0 representing red or any other method such as boolean variables. This tree uses the local tree balancing technique, and ensures no path through the tree is twice as long as any other. 

For a binary search tree to be a red-black tree it has to suffice the five conditions mentioned below.

•  Every node in the tree is either red or black 
• The root is always black. 
• Every leaf(which is a  NIL node in this case) is black. 
• If a node is red both its children(and its parent) is black. 
• For each and every node in the tree, all path from the node to descendant leaves contain the same number of black nodes. 

The first two points in the above definition is related with the coloring of the nodes in the tree. The third point introduces a new node called a NIL node. A detailed explanation about the NIL node is given below. 

NIL Node 

In red-black trees all leaf nodes and the parent of the root are NIL nodes. NIL nodes does not hold any value and it is always black. They are just a place holder and it comes into the equation in some cases of deletions and insertions. The tree in figure 1 depicts a red-black tree with these sentential nodes.

Figure 1: A Red-black tree with the NIL nodes

When operating on the red-black tree for ease and clarity we omit these from the diagrams unless it is really necessary. The figure 2 has the same tree as in figure 1 without the sentential nodes. We will be using the diagram depicted below to represent red-black trees from here on in unless stated.

Figure 2: A Red-black tree (drawn without the NIL nodes)

Red-black trees insertions and deletions are carried out in accordance with the five properties mentioned above. 

Black Height

The number of black nodes from a given node(X) down to a leaf excluding the node itself is called the black height. The property five of the red-black tree clearly defines this property. Each and every node should have the same black height when we compare the left subtree and the right subtree. 

Ex:- The black height of the node with the value 45 is 1 (2 if one considers the leaf node). If observed clearly this is true for each given path. This can be denoted as bh(x) where X being the node being considered. Therefore bh(45) is 1. 

Inserting into a Red-Black Tree

Insertions are identical to that of binary search trees but all the newly inserted nodes are red. If the parent of the newly inserted node is black no problems will arise. But if the parent is red then the fourth red-black property is violated. Hence the red black tree property should be resurrected. Five red-black property violations arise as a result of insertions but we only need to consider three because of symmetry.

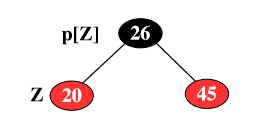
(i) Newly inserted node's     uncle   is red:-   The figure 3 (a) and (b) illustrates this violation after the new node with the value 26 (or 5) is inserted.

Figure 3: RBT property violation after inserting the value (a) 26 (b)  5

In the figure 3 the uncle of the node in question (z) is marked as u and p[z] and p[p[z]] stands for the parent and the grandparent respectively. This property violation can be fixed by recoloring of the nodes in the following order. 

•  The color of Z's uncle U and its parent p[Z] is changed from red to black 
• The grandparent (p[p[Z]]) of Z is colored red. 
• Update Z so now it points to the grandparent (new Z) of the initial setting 
• Keep repeating the above steps until the red-black property is resurrected or the new Z reaches the root. 
• If  the root was colored red recolor it to black. 

Figure 4 (a) and (b) shows the resulting tree after the recoloring (or color swaps)

Figure 4: Partial fix (when new Z is red) to a case 1 insertion problem

If   new Z   is not the root and p[new Z] is not red the fix ends at this point  . But the red-black property of the trees in figure 4 is not preserved. The root of the trees above is red but it should be black as per the second red-black tree property. The trees after the complete fix is given in figure 5.

Figure 5: RBT's after the case 1 fix

This fix does not take into account whether the new node( Z or the node which violates the red-black property) is the left or the right child. 

(ii) Newly inserted node's (Z) uncle is black and Z is a right child:- This is a complex case which requires rotations. Figure 6 (a) illustrates this red-black property violation. Keep note that this case has a symmetrical formation where the uncle is black and the Z is a left child. To reduce this complex case in to a simpler case the following steps are carried out in the order mentioned below. 

• Left (or right) rotate Z about its parent p[Z] which results in the tree in figure 6 (b). 
• Update Z so now it points to the parent of Z in the initial setting.

Figure 6: (a) RBT before the left rotation (b) Tree after the left rotation 

In the above example the uncle of the newly inserted node 26 is the NIL node. By definition NIL node is always black. So a left rotation is performed on the node containing the value 26 about its parent 20 and the resulting tree is given in figure 6 (b). Note that the red-black property violation still remains after the rotation. The resulting violation is the case 3 violation. So technically the rotation have reduce the complex violation into much simpler case.

 (iii) Newly inserted node's (Z) uncle is black and Z is a right child:- This scenario can occur as a result of a direct insertion of a node or as by product of a case 2 violation.  To fix this violation the following step are performed.

•  Right (or left) rotate p[Z] about p[p[Z]] 
• Swap the color of p[Z] to black and p[p[Z]] (now the sibling of z) to red 

Figure 7 (a) illustrates the tree before the right rotation and 7(b) depicts the tree after the rotation but before the colors are swapped.

Figure 7: (a) RBT before the right rotation (b) Tree after the right rotation 

The tree in figure 8 depicts the tree after the fix. Note that this case does not fall through to another case nor recursively move up the tree. This case terminates at this point after the rotation and the color swap.

Figure 8: RBT after the case 3 fix.